For a PM component the ER is defined as:
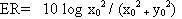
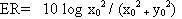
where
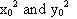
are the intensities on the slow and fast axes respectively and phase is not considered.
The complete description requires reference to more general elliptical polarization such as Stokes Parameters and the Poincare Sphere. Google will bring up many excellent references, two of which have been summarized here for comparison with ER.
http://en.wikipedia.org/wiki/Stokes_parameters
http://scienceworld.wolfram.com/physics/StokesParameters.html
Figure 2 illustrates the polarization ellipse within a rectangle of sides
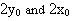
where
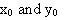
are the amplitudes of the slow and fast axis, and having major and minor axes a and b with phase difference
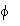
between the slow and fast axis beams.
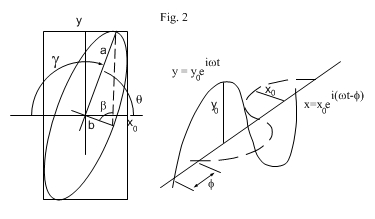
Figure 3 shows the Poincare sphere and the related Stokes Parameters
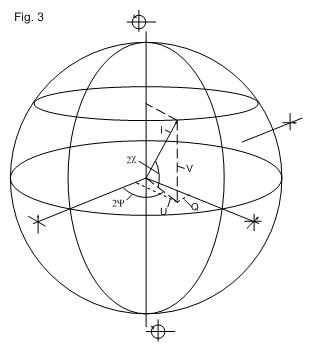
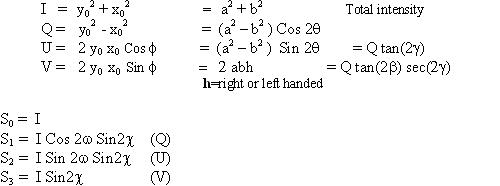
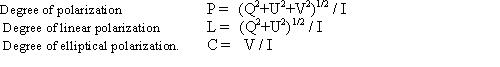
It can be shown that
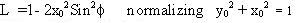
So the departure from linear or plane polarization is
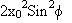
which can be regarded as a modified Stokes parameter and taken as
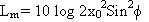
for comparison with ER.
When
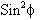
approaches zero the output is plane polarized at angle theta to the slow axis.